Statistics in Archaeology
Thomas Huet (University of Oxford, EAMENA project)
Introduction



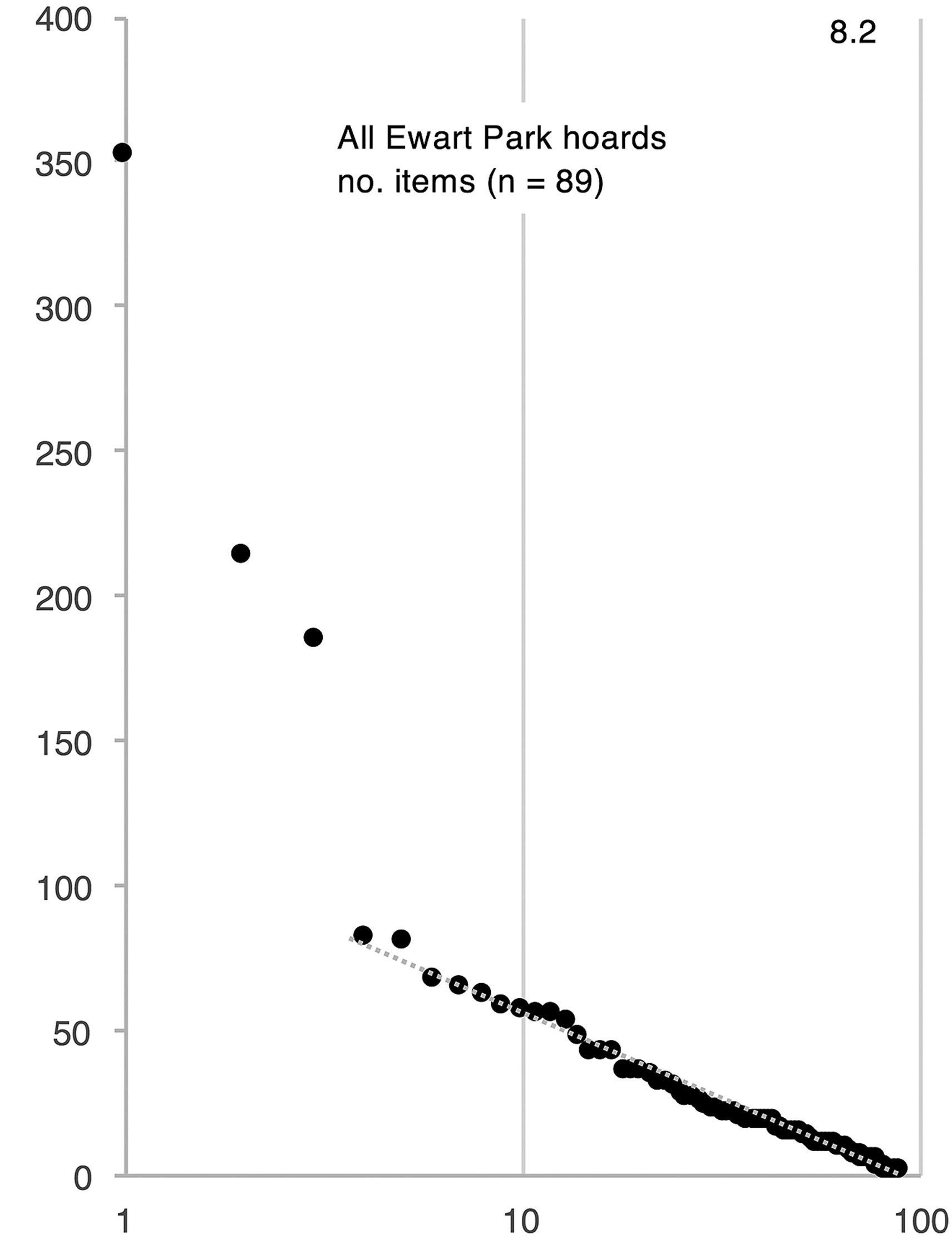
Inequalities
Historiography of Archaeology 1/2
| Start | Method | Description |
|---|---|---|
| 1850s | Prehistory | evolution, geology, anthropology |
| 1950s | Culture-Historical | similarities, typology, chronology |
| 1960s | New archaeology | chain operative, statistics, chronology (C14) |
| 1980s | Post-processual | dissimilarities, cultural relativism |
| 2020s | Tool-driven | Big data, ML / DL, aDNA |

Historiography of Archaeology 2/2


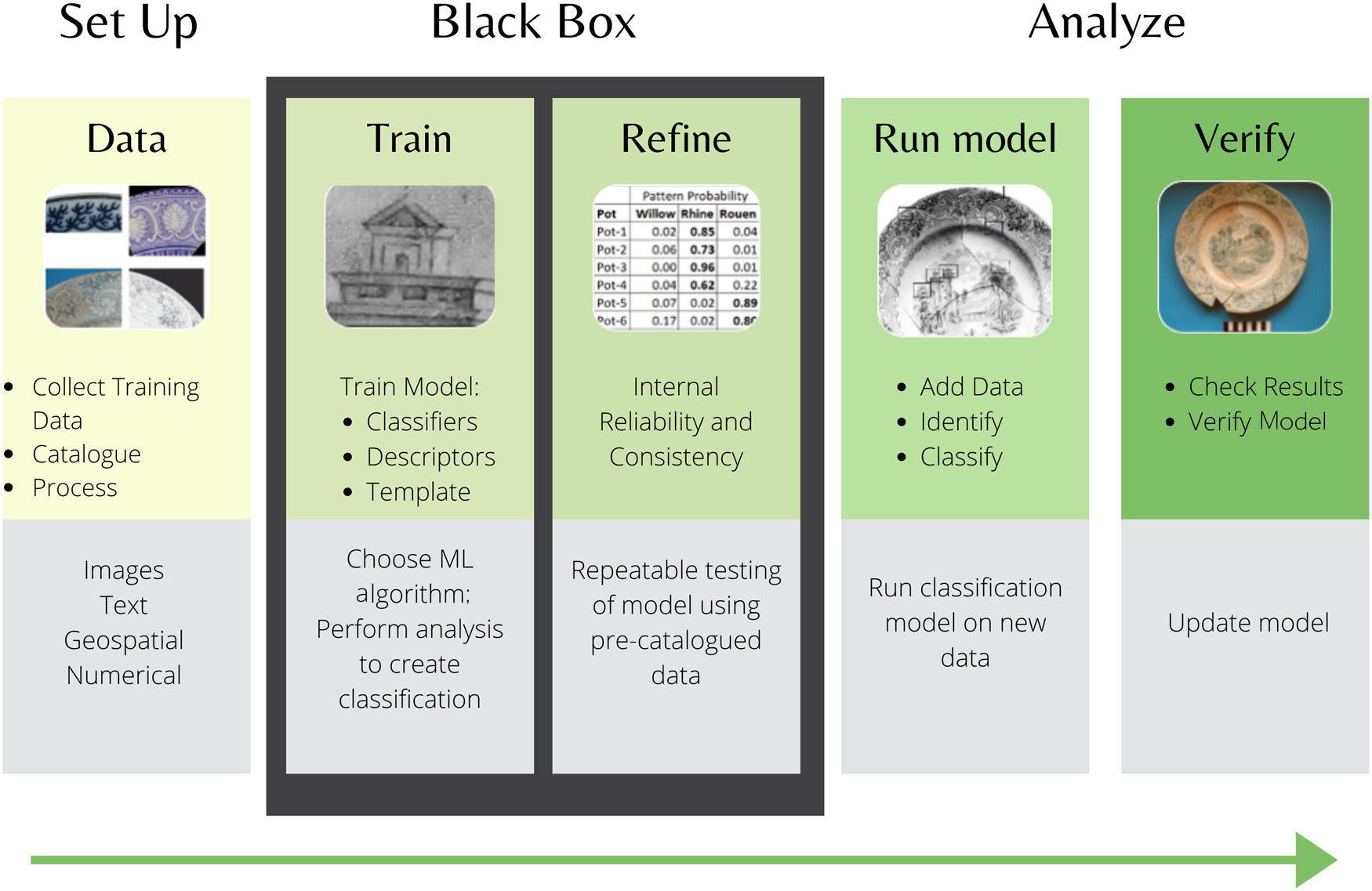
With the development of computational archaeology (e.g. AI/ML, aDNA) and oceans of data, the archaeologist becomes a research software engineer. A single project probably cannot exploit the full potential of the data at hand. Data is managed and made FAIR2 to produce serendipity over the long term.
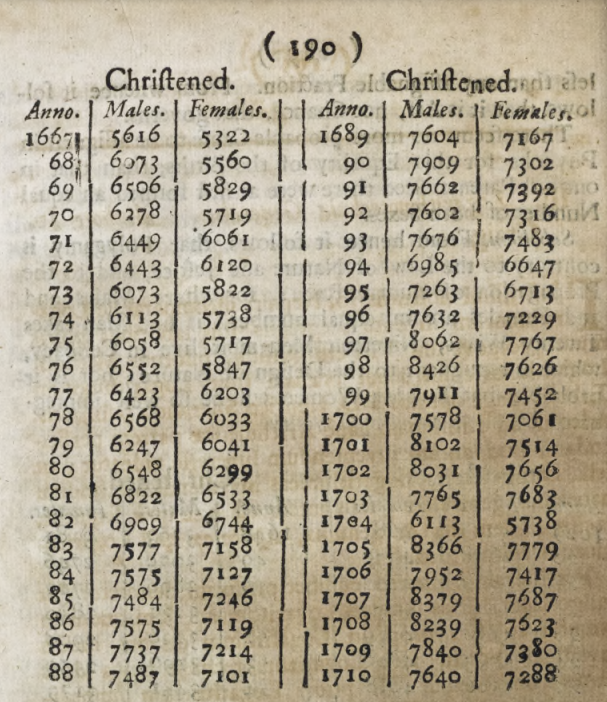
Birth of statistics



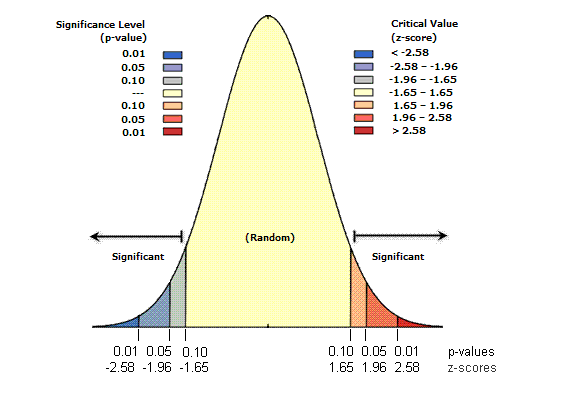
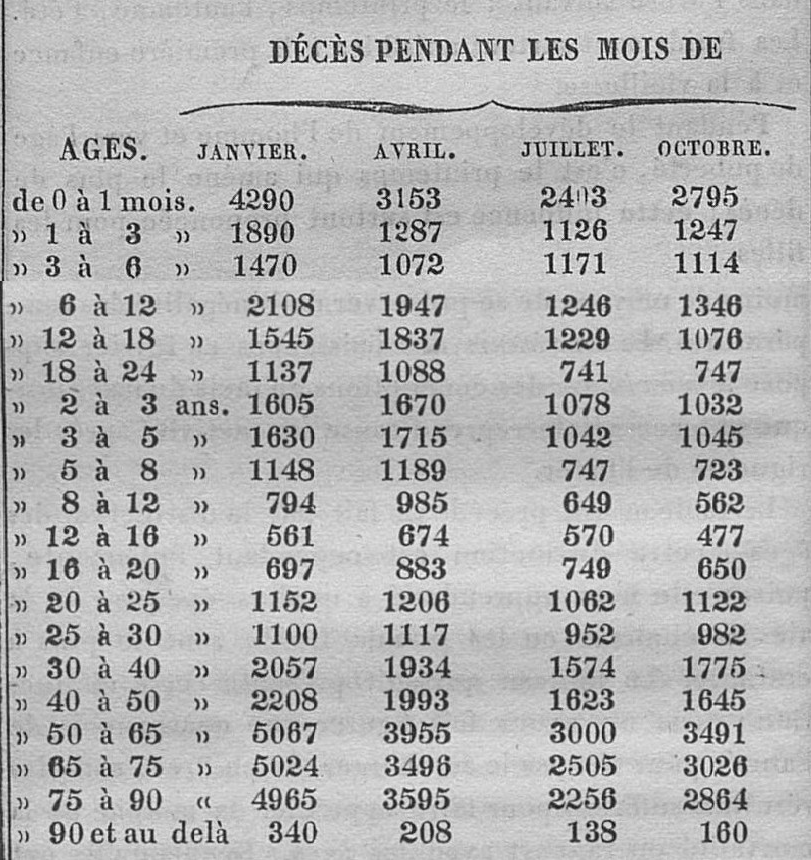

Advanced statistics

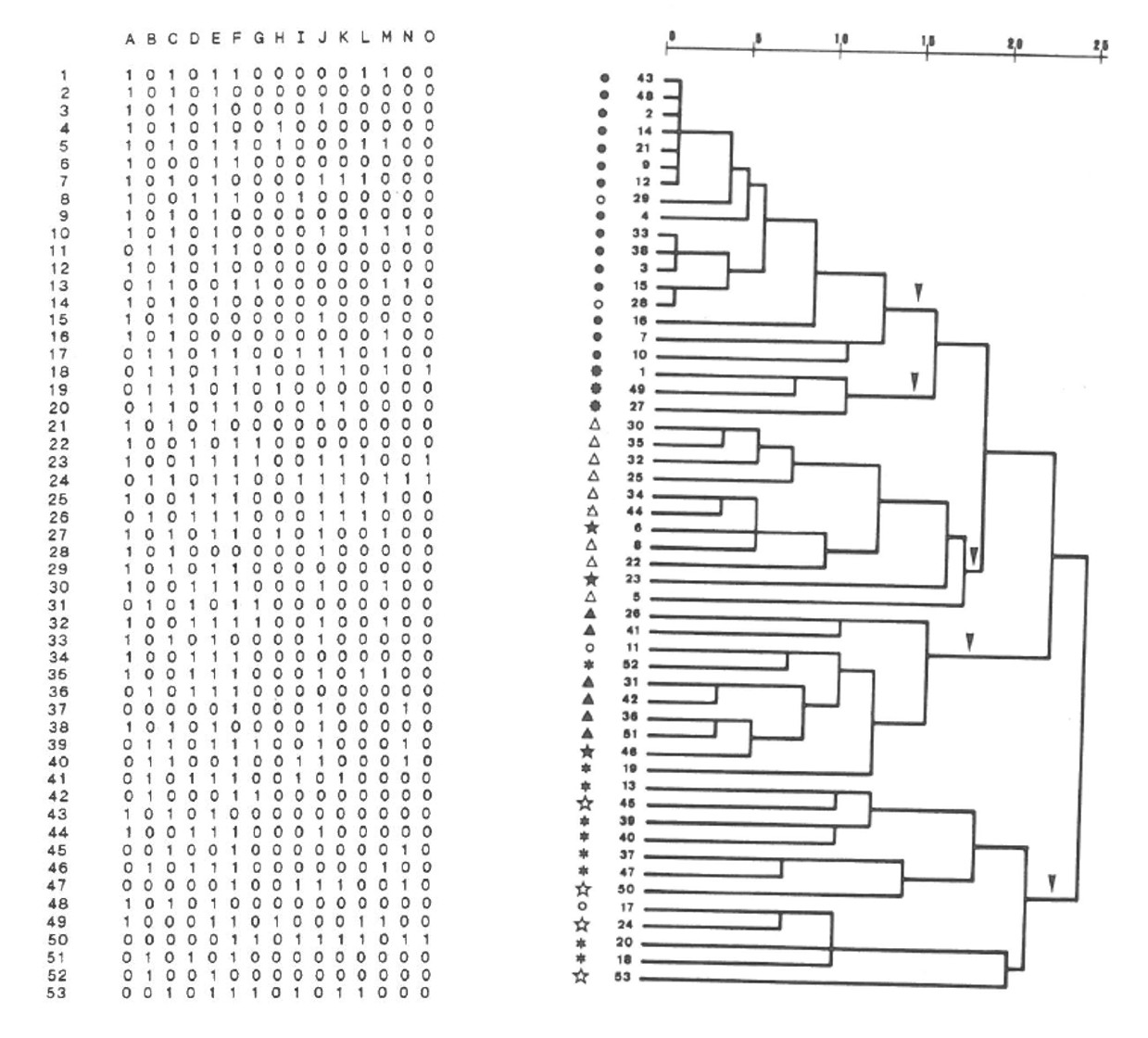
Artificial Intelligence & Machine Learning
Glossary of statistics
Type of statistics
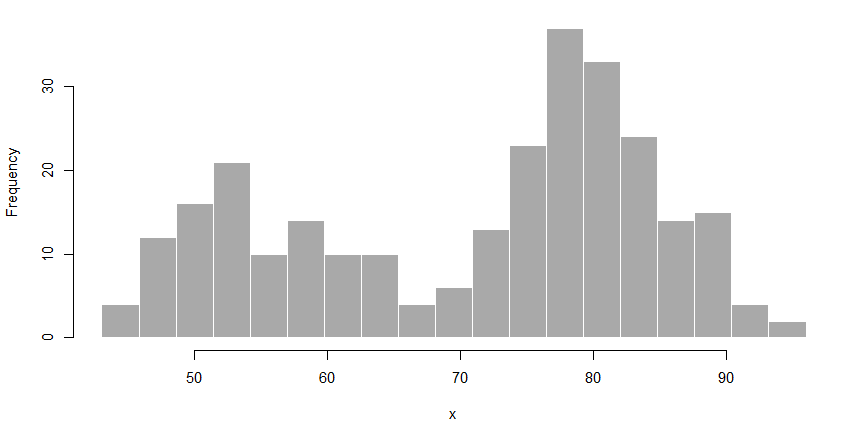
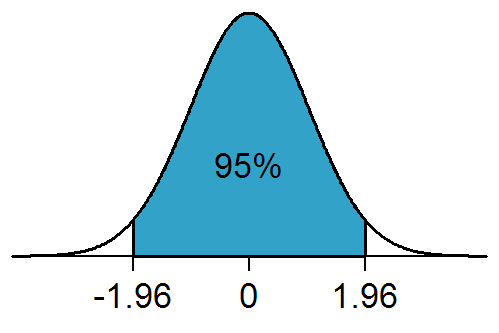
Describe the population with the mean (μ), the median (M) and standard deviation (σ)

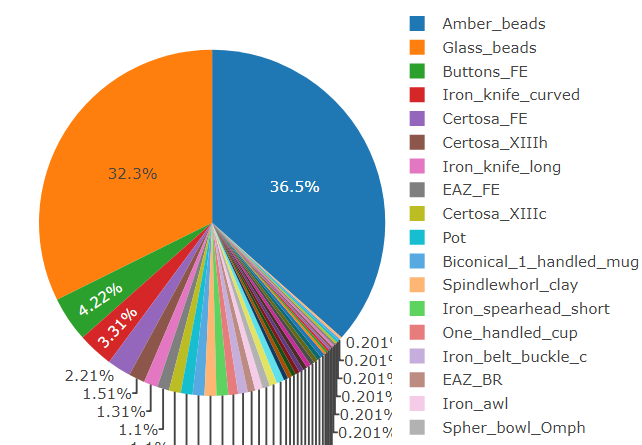



- conformity3 between the observed population and a theoretical distribution (e.g. normal law)
- homogeneity between different populations
- relation between several variables from the same population
Middle Range Theories
Archaeology establishes facts and proposes models to connect these facts
Robert K. Merton, 1968
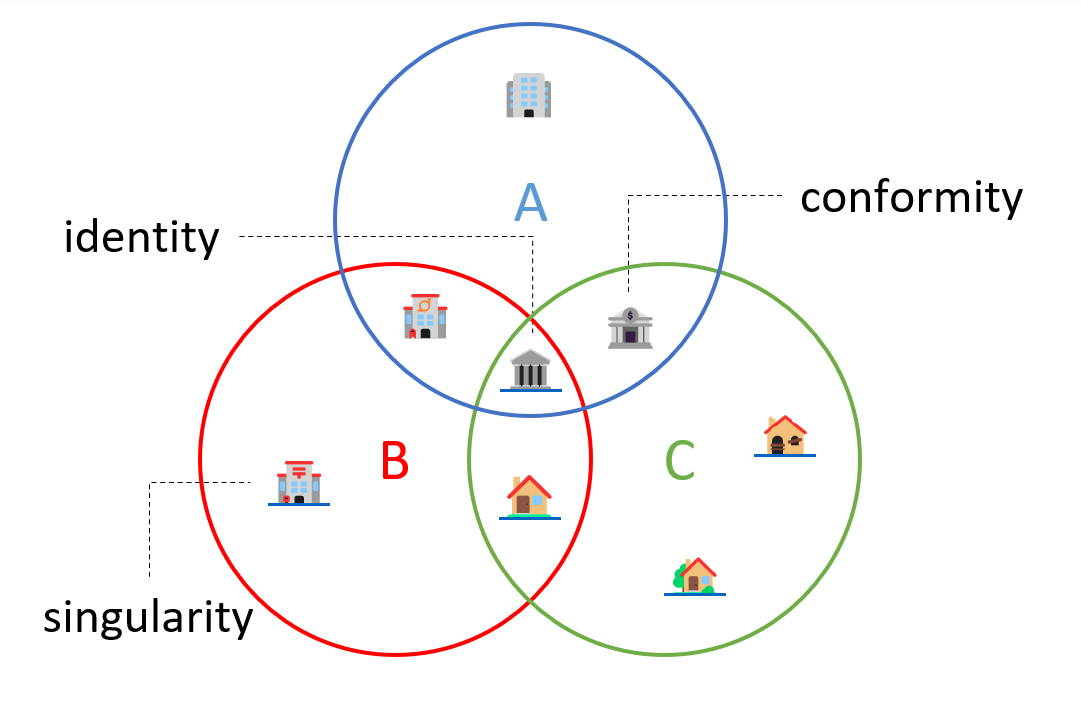
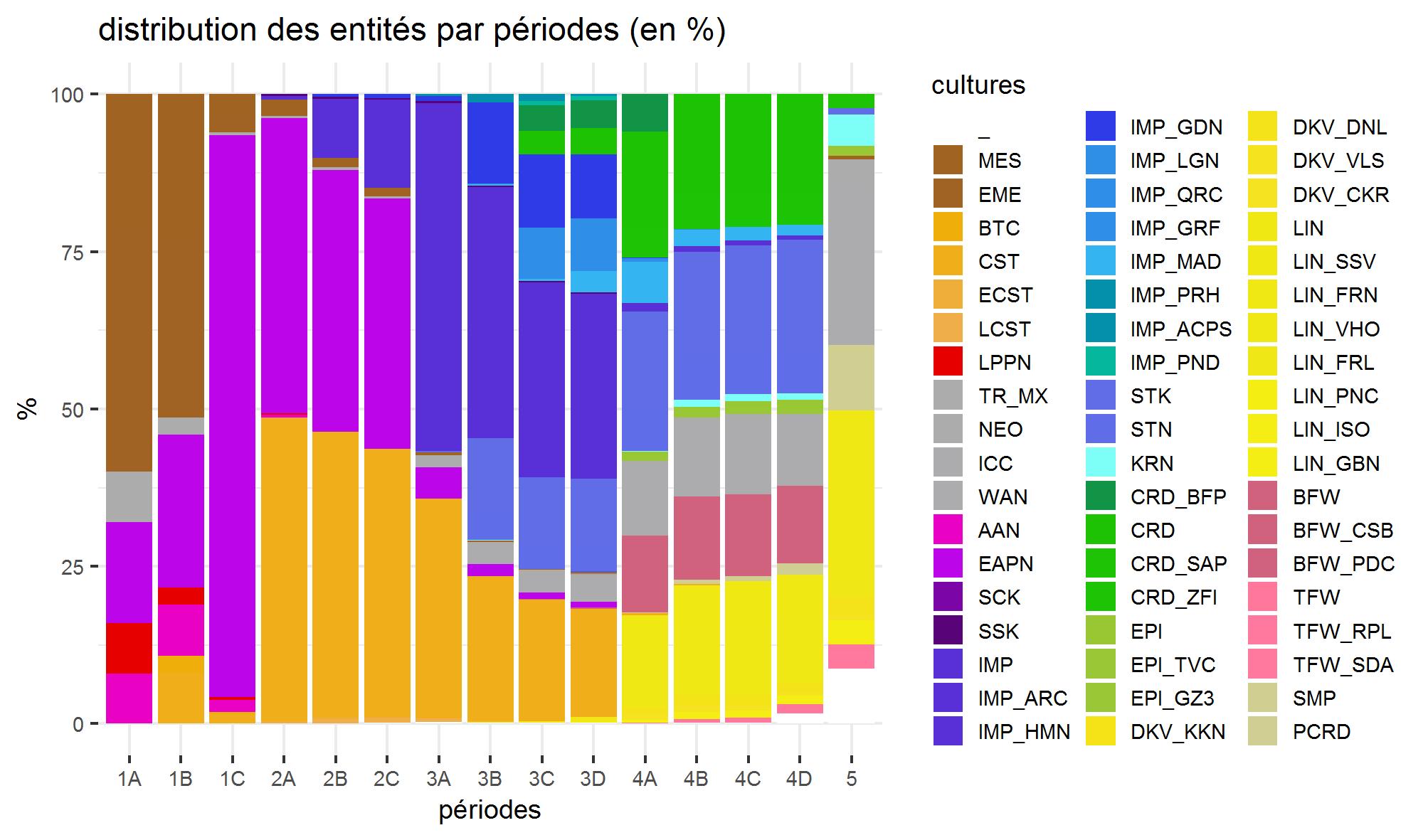
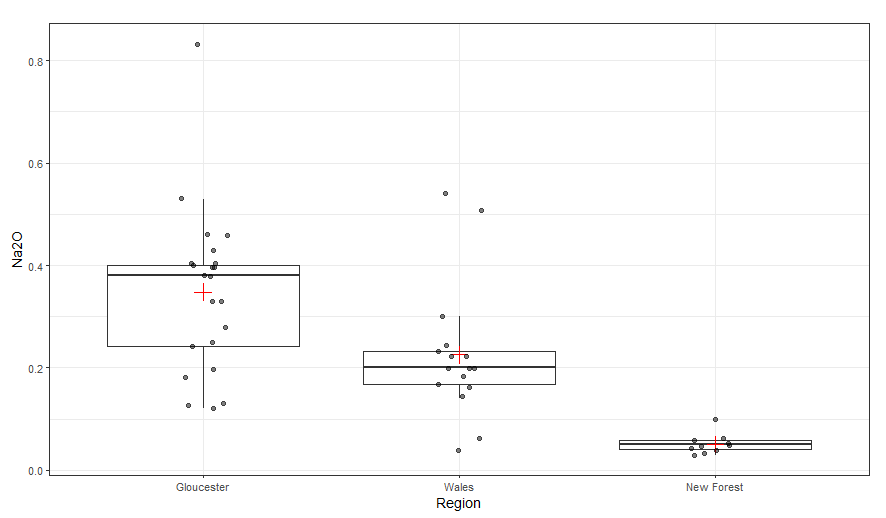
We want to compare 3 different archaeological cultures5 (groups of settlements, sites, geographical regions, chronological periods, etc.): A, B, and C


️

️
Entities

Tobler, 1970





Conformity


| A | B | C | |
|---|---|---|---|
| A | 0.00 | 3.24 | 2.53 |
| B | 3.24 | 0.00 | 1.05 |
| C | 2.53 | 1.05 | 0.00 |

Khi-square
χ 2
- Observed numbers
Code
| patient | virus.A | virus.B | virus.C |
|---|---|---|---|
| Mal.1 | 12 | 7 | 11 |
| Mal.2 | 19 | 7 | 4 |
| Mal.3 | 13 | 10 | 5 |
- Calculation of rows and columns sums
Code
df.copy <- df
df.copy <- rbind(df.copy, colSums(df.copy[ , -1]))
df.copy[nrow(df.copy), "patient"] <- "col.sum"
df.copy <- cbind(df.copy, rowSums(df.copy[ , -1]))
colnames(df.copy)[ncol(df.copy)] <- "row.sum"
kable(df.copy) %>%
kable_styling(full_width = FALSE, position = "center", font_size = 24) %>%
column_spec(ncol(df.copy), bold = TRUE) %>%
row_spec(nrow(df.copy), bold = TRUE)| patient | virus.A | virus.B | virus.C | row.sum |
|---|---|---|---|---|
| Mal.1 | 12 | 7 | 11 | 30 |
| Mal.2 | 19 | 7 | 4 | 30 |
| Mal.3 | 13 | 10 | 5 | 28 |
| col.sum | 24 | 20 | 44 | 88 |
- Calculation of expected numbers (E)
Code
| virus.A | virus.B | virus.C | patient |
|---|---|---|---|
| 15 | 8.18 | 6.82 | Mal.1 |
| 15 | 8.18 | 6.82 | Mal.2 |
| 14 | 7.64 | 6.36 | Mal.3 |
- Differences between expected (E) and observed (O) numbers
Code
| virus.A | virus.B | virus.C | patient |
|---|---|---|---|
| -0.77 | -0.41 | 1.60 | Mal.1 |
| 1.03 | -0.41 | -1.08 | Mal.2 |
| -0.27 | 0.86 | -0.54 | Mal.3 |

- Khi-2 calculation
Code
khi2.df <- matrix(nrow = length(df$patient),
ncol = length(df$patient))
colnames(khi2.df) <- rownames(khi2.df) <- df$patient
khi2.df[1 , 2] <- round(chisq.test(df[, c(2, 3)])$p.value, 2)
khi2.df[2 , 1] <- round(chisq.test(df[, c(2, 3)])$p.value, 2)
khi2.df[1 , 3] <- round(chisq.test(df[, c(2, 4)])$p.value, 2)
khi2.df[3 , 1] <- round(chisq.test(df[, c(2, 4)])$p.value, 2)
khi2.df[2 , 3] <- round(chisq.test(df[, c(3, 4)])$p.value, 2)
khi2.df[3 , 2] <- round(chisq.test(df[, c(3, 4)])$p.value, 2)
khi2.df <- as.data.frame(khi2.df)
color.me <- which(khi2.df < .1)
kable(khi2.df) %>%
kable_styling(full_width = FALSE, position = "center", font_size = 24) %>%
column_spec(1, bold = TRUE)| Mal.1 | Mal.2 | Mal.3 | |
|---|---|---|---|
| Mal.1 | NA | 0.47 | 0.08 |
| Mal.2 | 0.47 | NA | 0.22 |
| Mal.3 | 0.08 | 0.22 | NA |

H0: ✔️ accept homogeneity hypothesis
H1: ❌ reject homogeneity hypothesis
Coefficient
| cor | interpretation |
|---|---|
| 1 | … |
| 0.9 | oustanding |
| 0.8 | excellent |
| 0.7 | acceptable |
| 0.6 | weak |
| … | … |
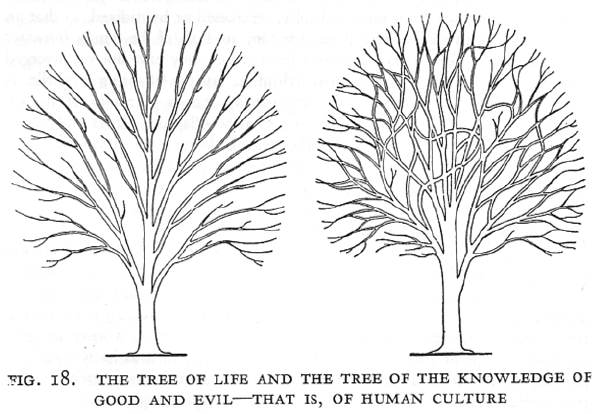
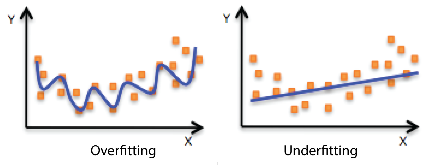
Models

Box, 1976
| propriety | description | example |
|---|---|---|
| Explanatory | not over- or under-fitting |
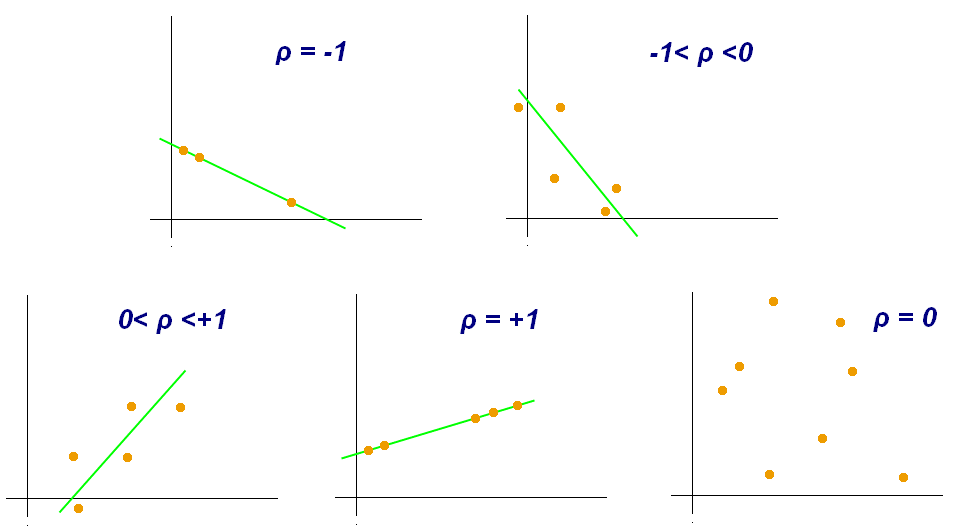
|
| Regularity | reproducing data regularity |

|
| Robustness | not sensitive to small changes in data |
|
| Parsimony | the simplest possible explanation is also the most probable |

|
| Versioning | carry its own story |

|
Models - Proprieties
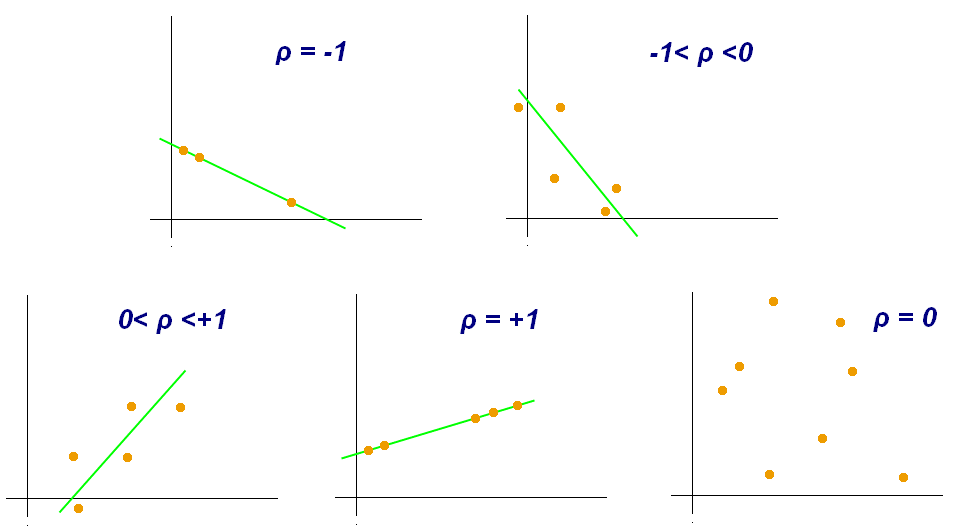




Data
Raw data - Primary data acquired via a device
Processed data - Working data (i.e. not definitive)
Aggregated data - Gathered data expressed in a summary form

Metadata - data about data

Code
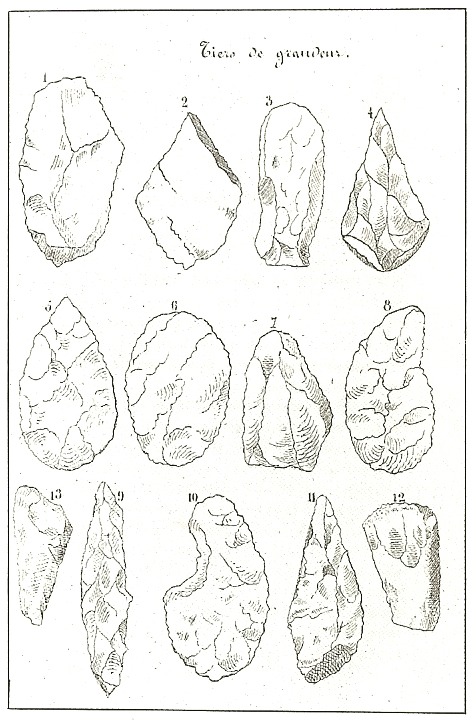
[1] "Caption-Abstract: Microliths (narrow blade type): Conistone Moor (Late Mesolithic c. 6000 BC) "[1] "Copyright: The Yorkshire Archaeological & Historical Society"
Missing data - Lack of knowledge, e.g. NA (Not Available)
Code
| Microliths | Scrapers | Burins | |
|---|---|---|---|
| site_A | 10 | 7 | 13 |
| site_B | 5 | 6 | 7 |
| site_C | NA | 10 | 4 |
| site_D | 2 | 5 | NA |
Sums by column (with NA)
Code
| Microliths | Scrapers | Burins |
|---|---|---|
| NA | 28 | NA |
Sums by column (without NA)
Code
| Microliths | Scrapers | Burins |
|---|---|---|
| 17 | 28 | 24 |
Boolean operators
Binary Topological Relationships
Scales



| from | to | transformation | example |
|---|---|---|---|
| Quantitative | Ordinal | discretization |
[1:10], [11:20], etc.
|
| Ordinal | Quantitative |
as.numeric()
|
"low" = 1, "medium" = 2
|
| Ordinal | Nominal |
as.factor()
|
Quantitative
Ordinal
Nominal
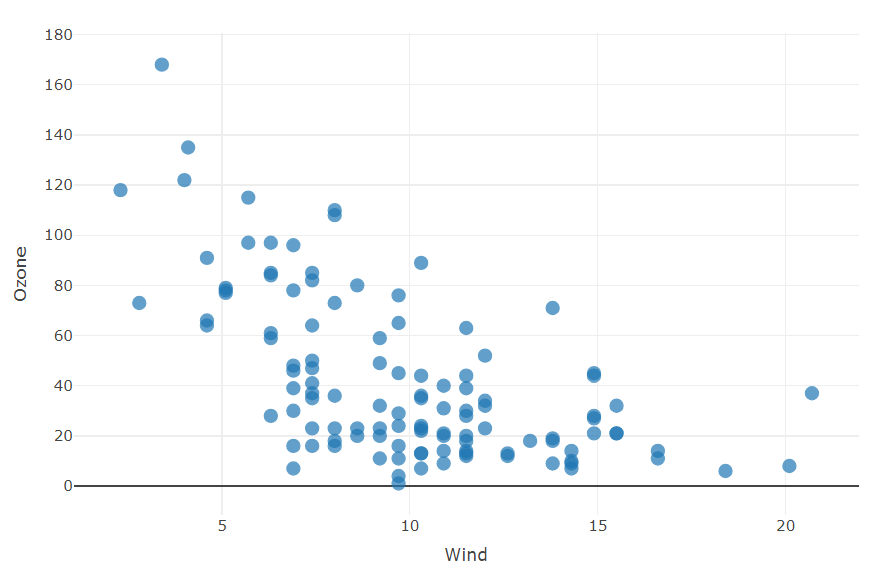
1-dim data
2-dim data
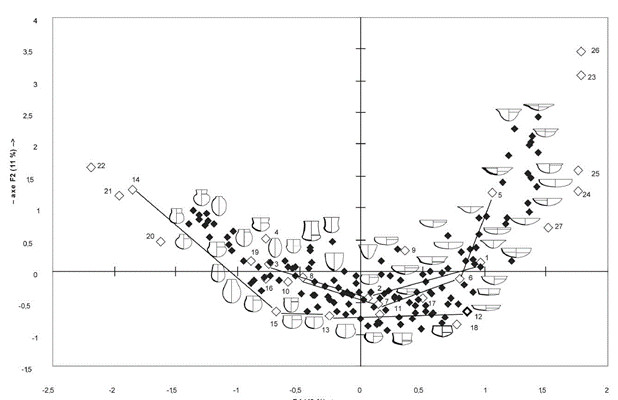
Hodder, I. 1974. A Regression Analysis of Some Trade and Marketing Patterns. World Archaeology 6: 172-189.
Hodder, I. and C. Orton. 1976. Spatial Analysis in Archaeology, pp 117-119. Dataset: archdata R package - OxfordPots dataset
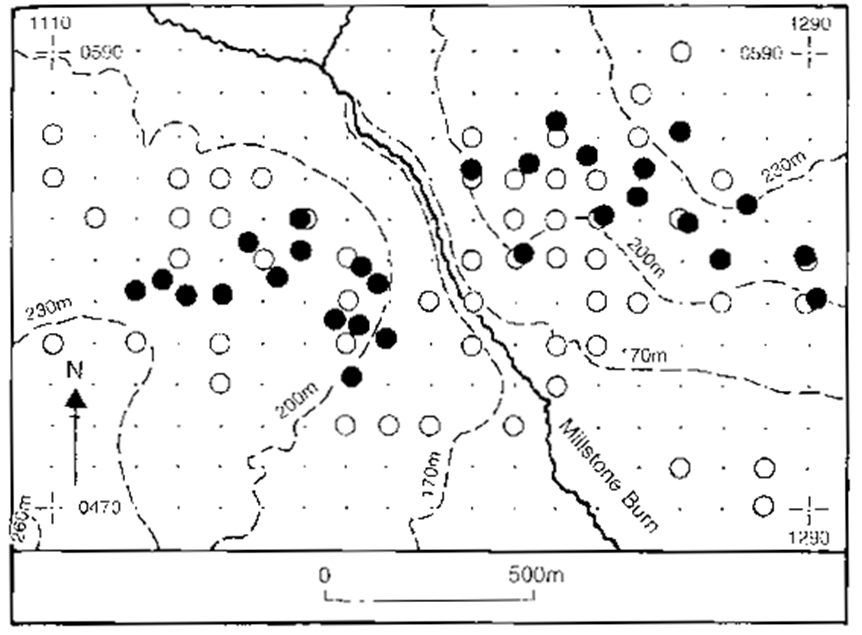
2-dim data spatial 1/3
2-dim data spatial 2/3
Average Nearest Neighbor Index (NNI)
| NNI | z.score | p.value | expect.mean.dist | observ.mean.dist | |
|---|---|---|---|---|---|
| random | 1.69 | 5.91 | 0 | 0.85 | 1.43 |
| cluster | 1.64 | 5.51 | 0 | 0.39 | 0.64 |
| regular | 2.67 | 12.75 | 0 | 0.84 | 2.24 |
2-dim data spatial 3/3
Random patterns versus Clustered patterns
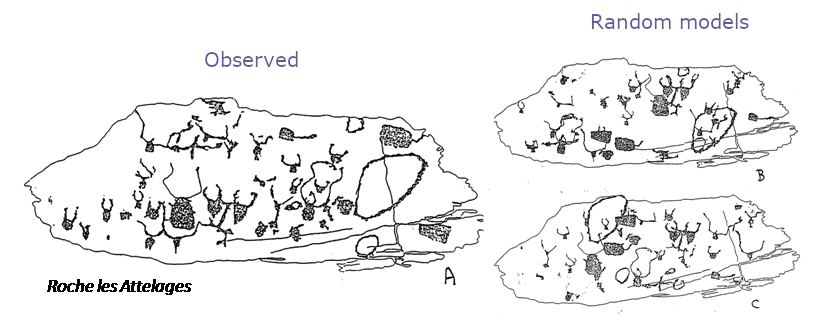
Regular pattern
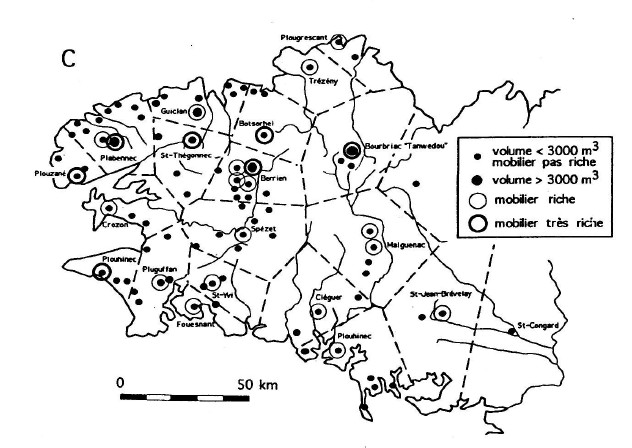
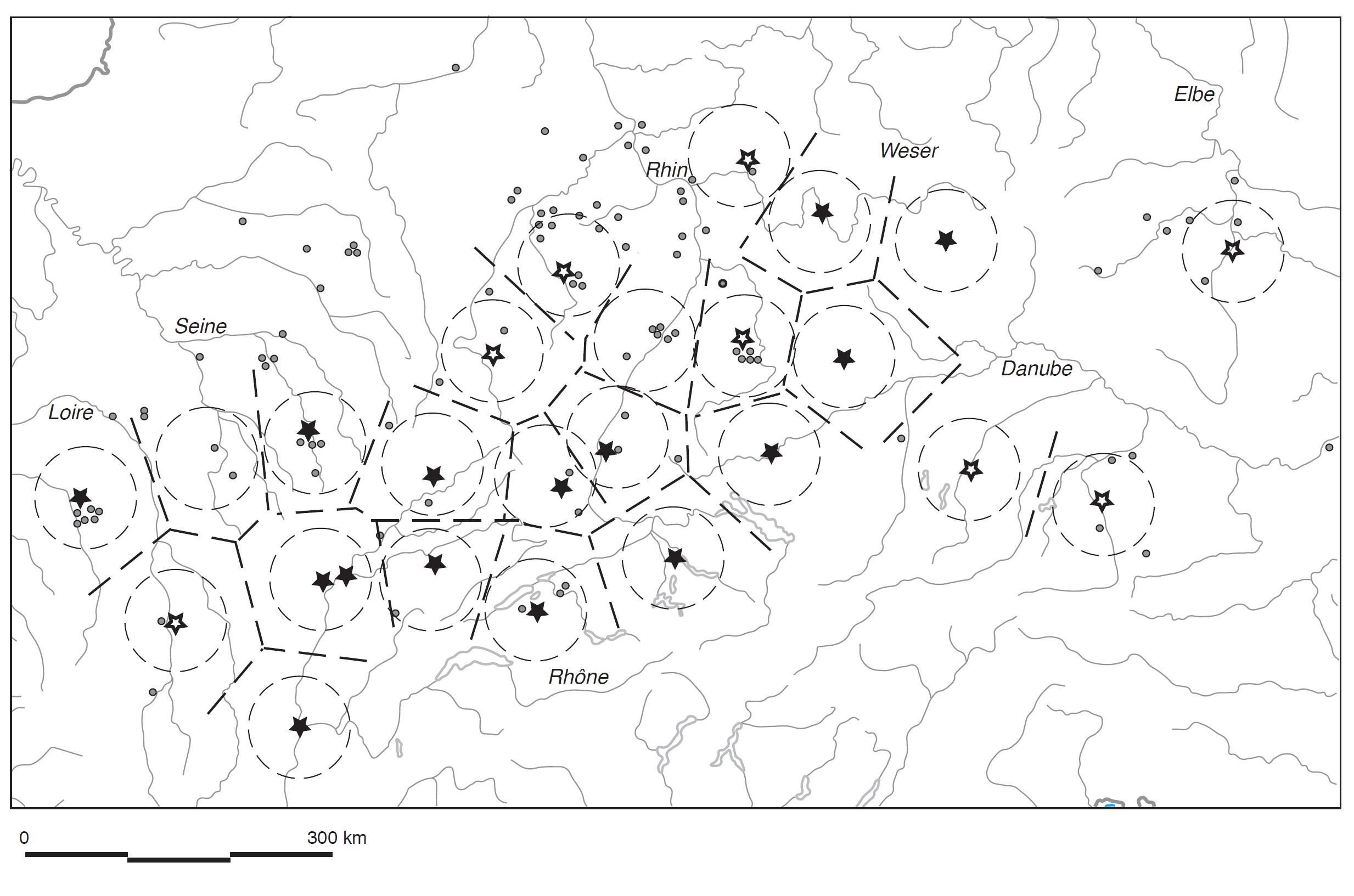
Gradient pattern
2-dim data shape
3-dim data
Current dataset: ANR Itineris
3-dim or more data


3-dim or more data
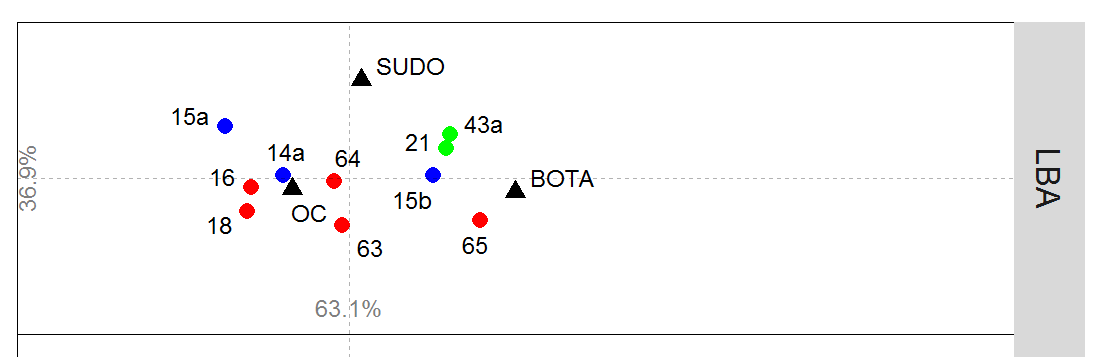
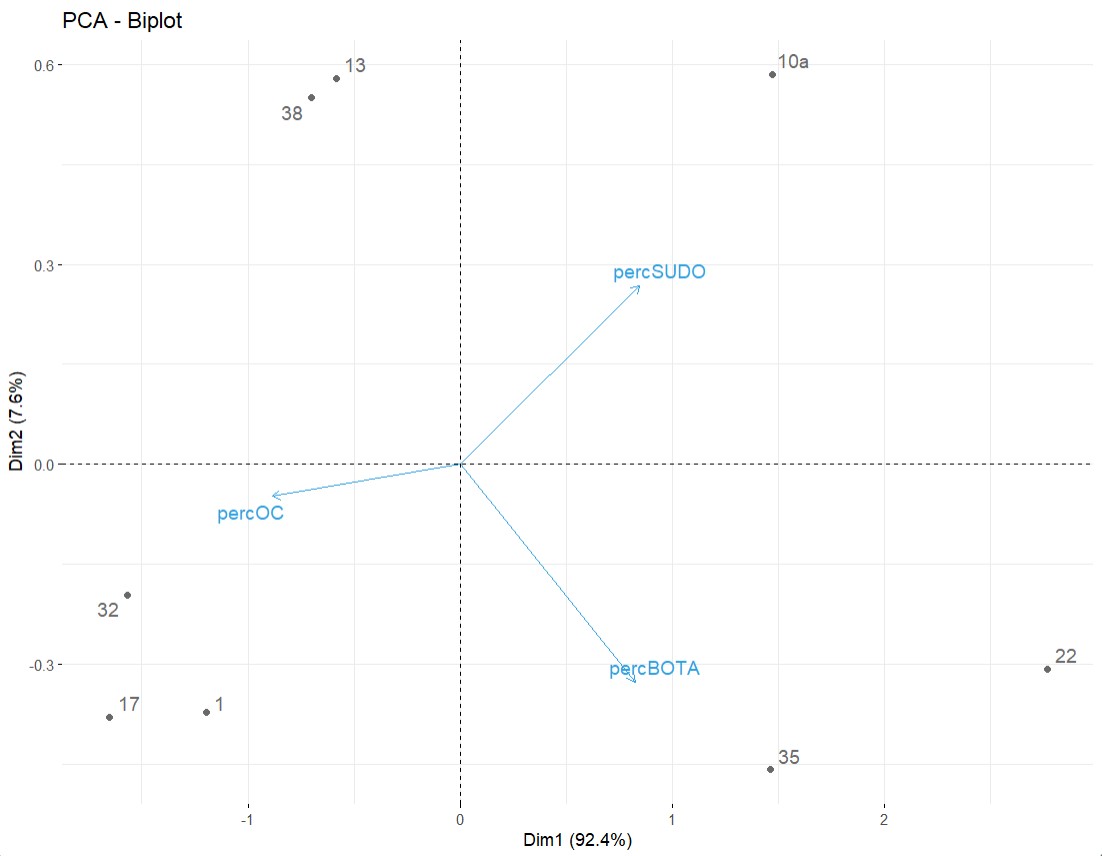

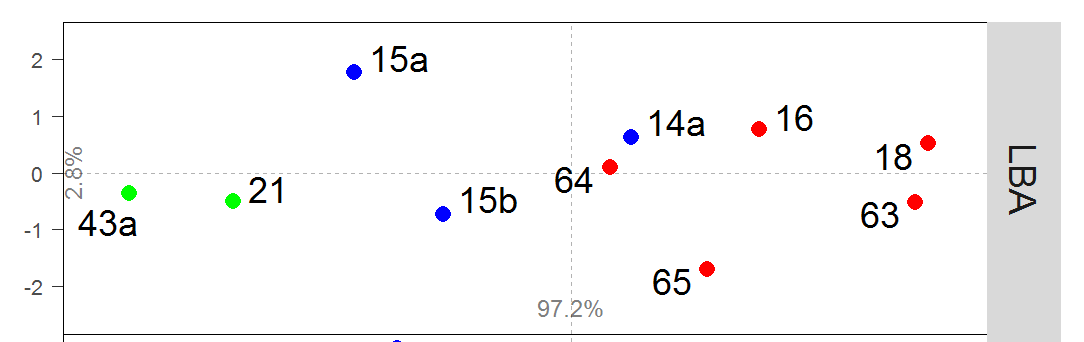
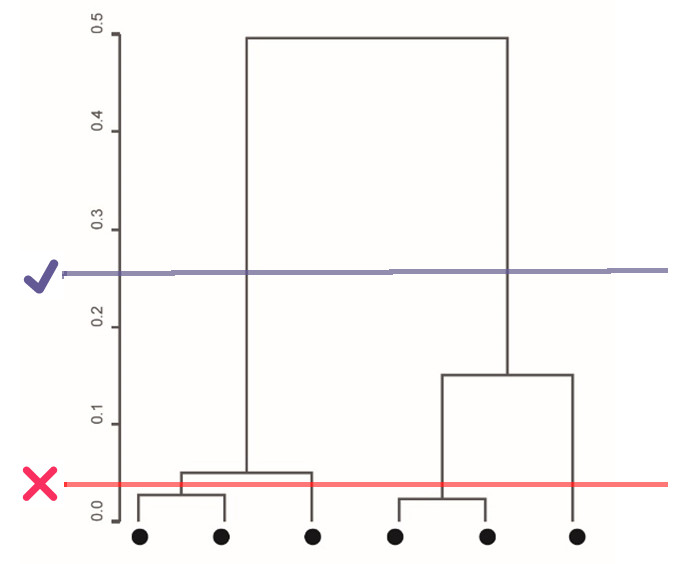
Seriation
Practice 
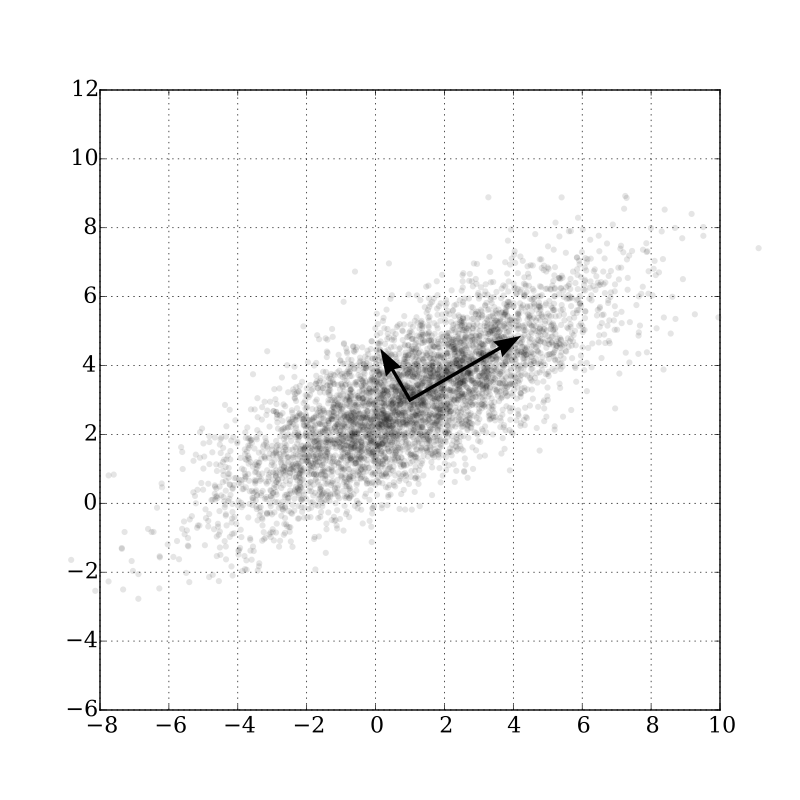
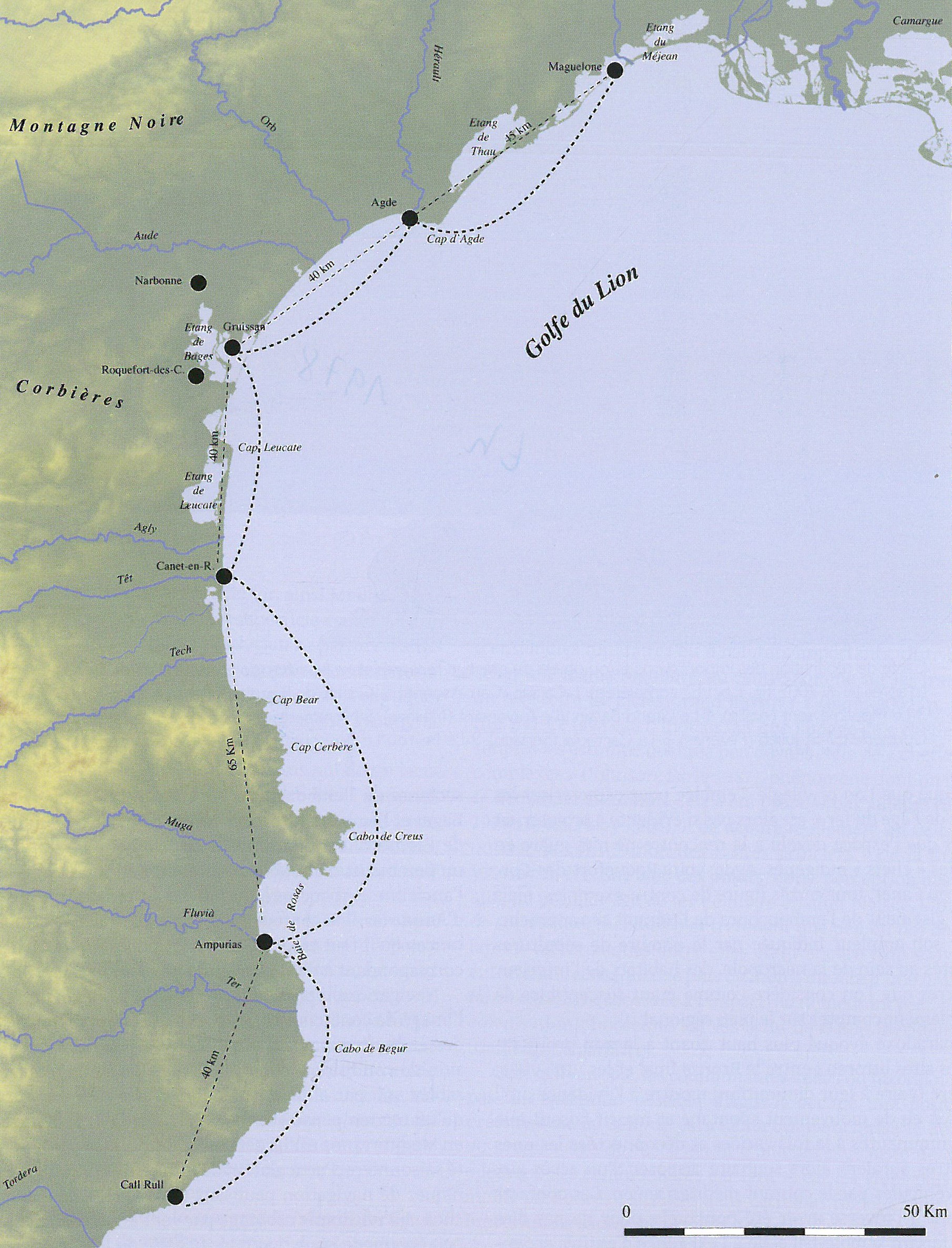
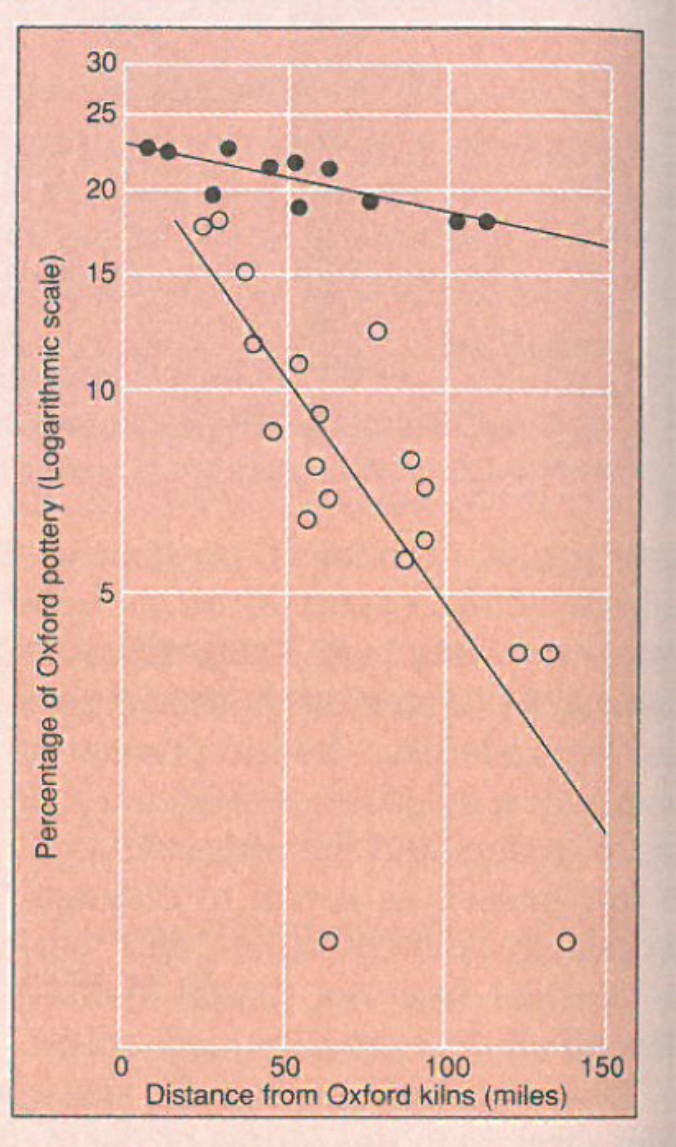
Use of the OxfordPots dataset (archdata R package), to reproduce the linear regression of Oxford potteries distribution by Fulford and Hodder7
R code:
install.packages("archdata")
library(archdata)
data("OxfordPots")
OxfordPots$OxfordPct.log <- log(OxfordPots$OxfordPct)
Oxford.water.transport <- subset(OxfordPots, WaterTrans == 1)
Oxford.water.transport.no <- subset(OxfordPots, WaterTrans == 0)
plot(x = Oxford.water.transport$OxfordDst,
y = Oxford.water.transport$OxfordPct.log,
xlim = c(0, max(Oxford.water.transport$OxfordDst)),
ylim = c(0, max(Oxford.water.transport$OxfordPct.log)),
pch = 16,
xlab = "Distance from Oxford kilns (miles)",
ylab = "Percentage of Oxford pottery (Logarithmic scale)")
points(x = Oxford.water.transport.no$OxfordDst,
y = Oxford.water.transport.no$OxfordPct.log)
abline(lm(OxfordPct.log ~ OxfordDst, data = Oxford.water.transport))
abline(lm(OxfordPct.log ~ OxfordDst, data = Oxford.water.transport.no))
https://github.com/zoometh/thomashuet/blob/main/teach/stats/stats/dim2/regression-basic.R
Bibliographic resources




Contact

Statistics in Archaeology  Université Paul-Valéry, Feb 2023 - Thomas Huet
Université Paul-Valéry, Feb 2023 - Thomas Huet
Footnotes
i.e. Post-positivism
Findable, Accessible, Reusable, Interoperable
i.e. goodness-of-fit
“Sociological theory, if it is to advance significantly, must proceed on these interconnected planes: (1) by developing special theories from which to derive hypotheses that can be empirically investigated and (2) by evolving a progressively more general conceptual scheme that is adequate to consolidate groups of special theories” Robert K. Merton, 1968
An archaeological culture is a polythetic assemblage of features more frequently associated with each other within a given area than outside it (Clarke 1968, Brun 1988, Shennan et al. 2015, etc.)
“people think closer things are more similar”, Montello et Fabrikant, 2006.
Fulford, M. G., & Hodder, I. (1974). A regression analysis of some Late Romano-British pottery: a case study. Oxoniensia, 39, 26-33.